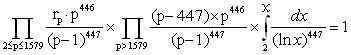
The first occurrence of the 447-tuples with a width of 3159
should be before x, where x is the solution to the equation
below.
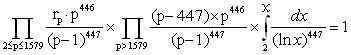
The products are over the primes in the ranges given. The
value of rp is the number of open residue classes for each
pattern of the 447-tuples. These values of rp are given in
the table 'Number of open residue classes'.
Calculations of the first product for each pattern are
as follows:
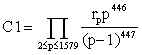
Value of first product |
|
| Pattern #1 | 2.98 x 10^343 |
| Pattern #2 | 2.23 x 10^343 |
| Pattern #3 | 3.79 x 10^343 |
| Pattern #4 | 3.17 x 10^343 |
| Pattern #5 | 7.21 x 10^343 |
| Pattern #6 | 5.96 x 10^343 |
| Pattern #7 | 2.98 x 10^343 |
| Pattern #8 | 2.23 x 10^343 |
| Pattern #9 | 3.79 x 10^343 |
| Pattern #10 | 3.17 x 10^343 |
| Pattern #11 | 7.21 x 10^343 |
| Pattern #12 | 5.96 x 10^343 |
The value of the second product was calculated using the
zeta function. The value of the second product is the
same for all patterns.
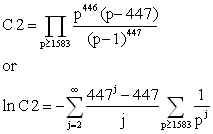
Value of second product |
|
| All Patterns | .000225 |
Finally, the value of x can be calculated by solving
the equation:
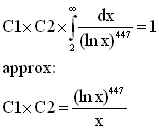
The calculated value of 'x' for each pattern of the
447-tuples are as follows:
First occurrence before |
|
| Pattern #1 | 1.53 x 10^1198 |
| Pattern #2 | 2.16 x 10^1198 |
| Pattern #3 | 1.15 x 10^1198 |
| Pattern #4 | 1.42 x 10^1198 |
| Pattern #5 | 5.33 x 10^1197 |
| Pattern #6 | 6.69 x 10^1197 |
| Pattern #7 | 1.53 x 10^1198 |
| Pattern #8 | 2.16 x 10^1198 |
| Pattern #9 | 1.15 x 10^1198 |
| Pattern #10 | 1.42 x 10^1198 |
| Pattern #11 | 5.33 x 10^1197 |
| Pattern #12 | 5.33 x 10^1197 |
By the Hardy-Littlewood k-tuples conjecture, about 12
instances of the 447-tuples with a width of 3159 can be
expected before 2.2 x 10^1198 .
The primorial of the first 407 primes (2 thru 2801) is equal
to 2.19 x 10^1197. The product of the number of open residue
classes for these 407 primes is 1.34 x 10^1024. If the sets
are evenly distributed then there is a chance (ever so
slight) that the first 447-tuple in a width of 3159 integers
could occur at about 1.6 x 10^174. Again, the primorial
of the first 84 primes (2 thru 433) is 5.5 x 10^176, and the
product of the number of open residue classes for these 84
primes is 7.8 x 10^65. Another words, checking 7.8 x 10^65
patterns 'could' find a violation set.
As shown above, finding a 447-tuple with a width of 3159 is
quite improbable using current prime testing methods.
The above calculations were performed using Ubasic.
Formulas from "Prime Numbers and Computer Methods for
Factoriazation" by Hans Riesel
© 2005 Thomas J Engelsma